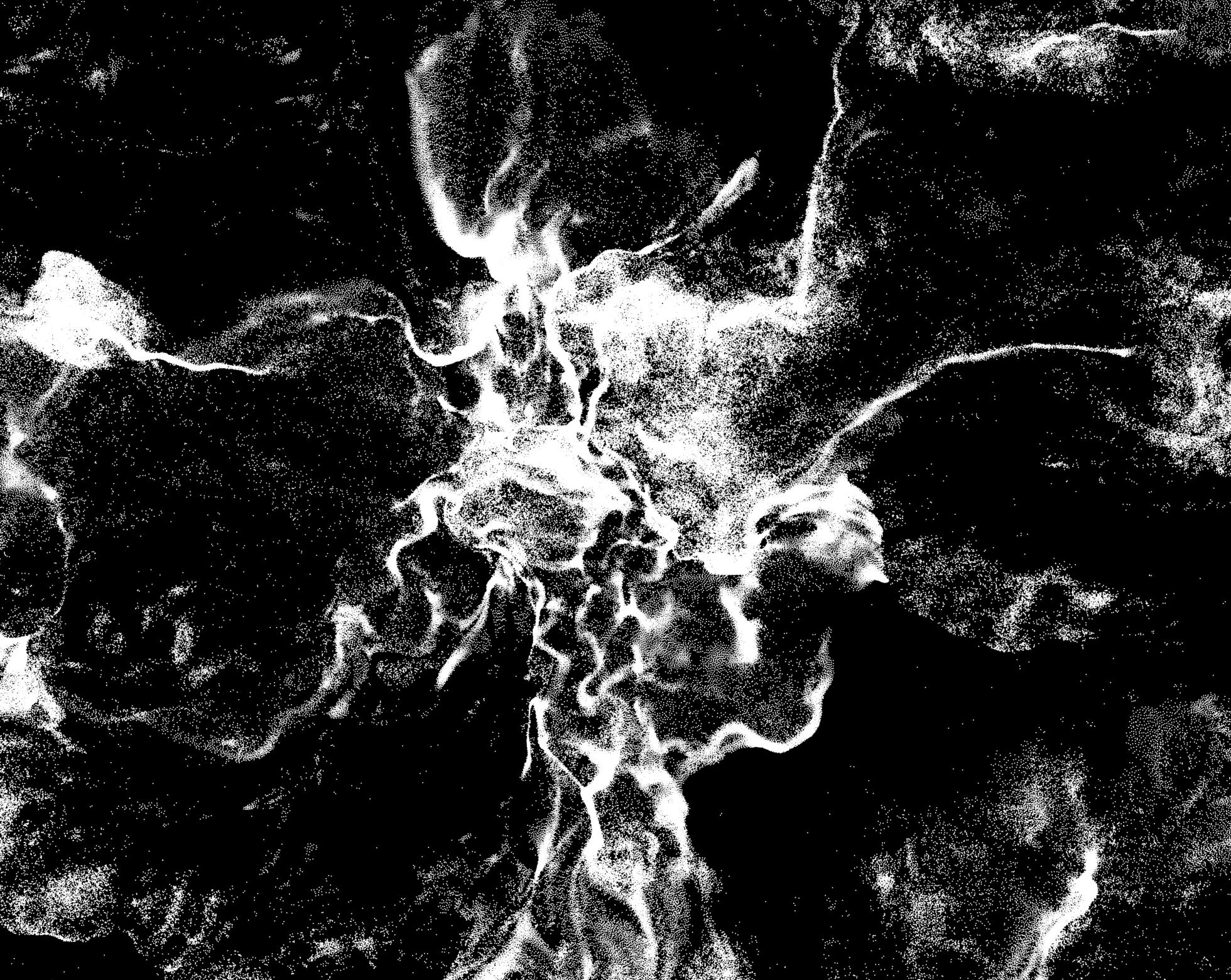
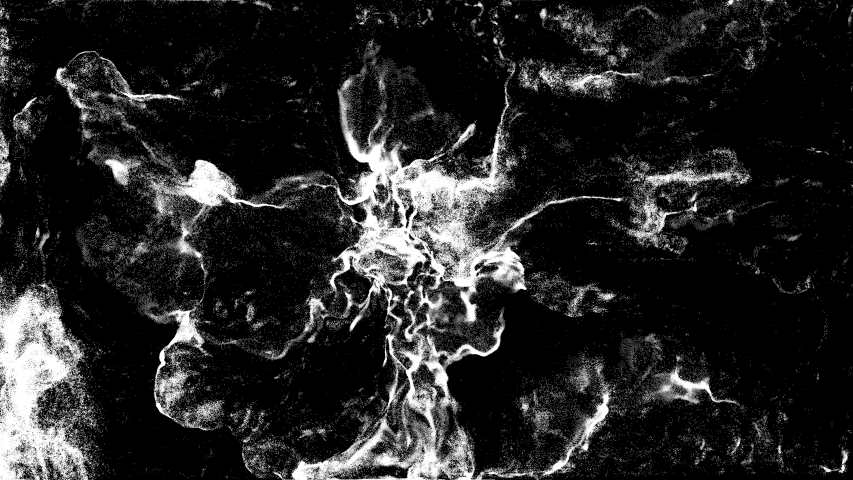
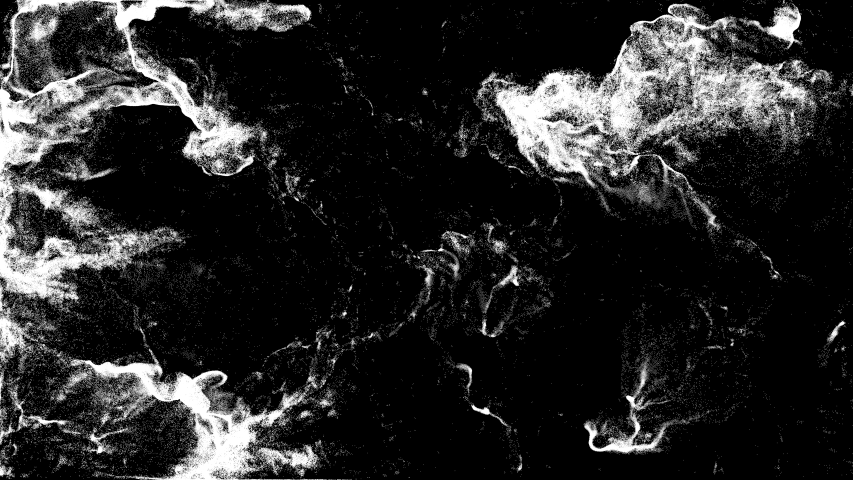
If there is beauty in these mathematical representations, it is because nature expresses itself directly in them. Far from distancing us from nature, these computer-generated images remind us of its beauty and allow us to see what we no longer see.
Navier-Stokes or the beauty of the crests
Find out more
The mathematician Henri Navier and the physicist George Gabriel Stokes defined an equation describing fluid motion through their respective works in 1823 and 1845. This equation, which is not well known to the general public, is still essential in computer graphics software and virtual fluid simulations.
If there is beauty in these mathematical representations, it is because nature expresses itself directly. Far from distancing ourselves from this nature, these computer-generated images remind us of its beauty and allow us to see what we no longer see.
The “crest” of the title of the work evoke of course the peaks of imaginary waves, but they also refer to the aesthetics of the film.
The spectator too is on a crest, caught between the awareness that what he is looking at is false – that it is only visual representations of equations – and the pleasure and magic of seeing points lost in space as liquids in motion.
“In the evidence of the waves, the eye is carried away by the dynamics of the white particles, surprised by the strength and speed of the waves. Sometimes it gets lost in a microbalance of dark matter ebb and flow.
Did the waves come from a hidden mountain?
Within the frame, the reefs dance. A succession of impulses, accelerations, hesitations.
The crests are created at the whim of the counter-currents and sieved the hollows.
The waves do not run out, their course is unrestrained; in this respect, they are rogues.
It would seem that the movement is constrained and that the loophole does not exist.
How long has this struggle been going on?”
Text translated from french, written by S.Z.
Votre contact


Merci pour votre contribution.
Vous serez informés de sa publication ou d’une éventuelle demande de compléments.